経済学におけるエッジワースボックスは、複数の個人が互いに利益を最大化するために財をどのように交換するかを考える上で、パレート最適な点を視覚的に表現するための便利な図です。
エッジワースボックスや契約曲線をわかりやすく解説!
エッジワースボックスの歴史的背景
この概念は、Francis Ysidro Edgeworthによって考案され、彼の名前にちなんで名付けられました。
彼は、アイルランド出身の哲学者兼政治経済学者で、統計学の方法において1880年代に重要な貢献をしました。
彼は効用についての理論を発展させ、無差別曲線や有名なエッジワースボックスを導入しました。
有名な著作は、「数理心理学(Mathematical Psychics)」であり、経済学における数学の応用について論じました。
エッジワースボックスを理解する前に:無差別曲線について思い出しましょう
無差別曲線とは、ある個人が同じ効用水準を達成できる財の組み合わせの集合です。
数学的にきちんと定義することにしましょう。2財しかない簡単な状況を考えます。
財\(x\)と財\(y\)の個数をそれぞれ\(q_x, q_y\)とします。
ある個人がいて、その人の効用関数を\(u\)で表すことにします。
このとき、効用水準\(\overline u \in \mathbb R\)を達成する無差別曲線は、
\begin{align*} \{(q_x, q_y) \mid u(q_x, q_y) = \overline u \}\end{align*}
です。
つまるところ、無差別曲線というのは、\(u\)という2変数関数の適当な高さの等高線です。
標準的にはですが、無差別曲線は次のような形状をしています。
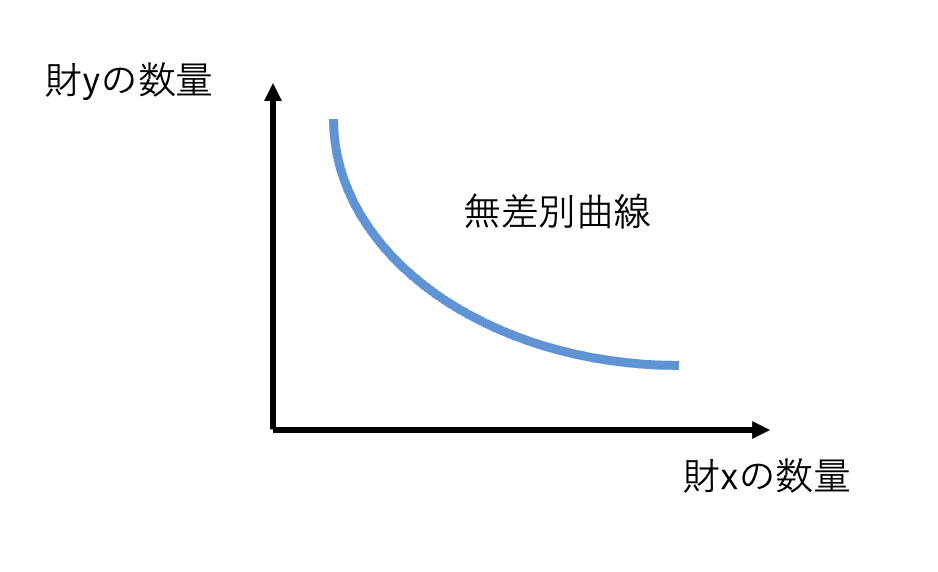
この青線の上の\(q_x, q_y\)の組み合わせであれば、効用は同じであるということです。
エッジワースボックスが用いられる状況設定
エッジワースボックスを理解するには、まず2人2財の純粋交換経済を考えることから始めます。
この経済では、2人の個人(AとB)が2つの財(財xと財y)が存在します。
財\(x\)は全部で\(q_x\)存在し、最終的に\(A, B\)がそれぞれ\(q_x^A, q_x^B\)個を手にします。
\begin{align*} q_x = q_x^A + q_x^B\end{align*}
です。
財\(y\)は全部で\(q_y\)存在し、最終的に\(A, B\)がそれぞれ\(q_y^A, q_y^B\)個を手にします。
\begin{align*} q_y = q_y^A + q_y^B\end{align*}
です。
\(A,B\)それぞれの効用を\(u_A, u_B\)で表すことにします。
\(A, B\)の無差別曲線をとなりに並べてみましょう。
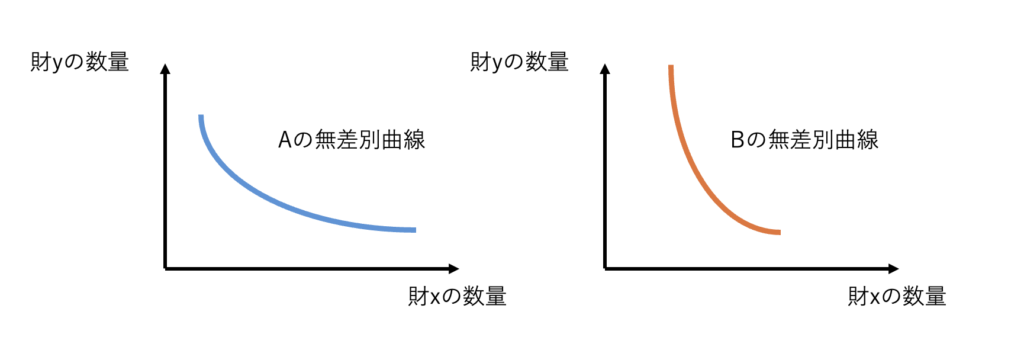
無差別曲線の形状は今ここで、適当です。考えたいことは、
\(A\)がやりたいことは、
\begin{align*} \textrm{maximize} u_A(q_x^A, q_y^A)\\ \begin{cases}q_x = q_x^A + q_x^B \\ q_x = q_x^A + q_x^B \end{cases}\end{align*}
です。
一方で、\(B\)がやりたいことは、
\(A\)がやりたいことは、
\begin{align*} \textrm{maximize} u_B(q_x^B, q_y^B)\\ \begin{cases}q_x = q_x^A + q_x^B \\ q_x = q_x^A + q_x^B \end{cases}\end{align*}
これを考えたいのですが、
\begin{align*} \begin{cases}q_x = q_x^A + q_x^B \\ q_x = q_x^A + q_x^B \end{cases} \end{align*}
の部分が考えにくいので、
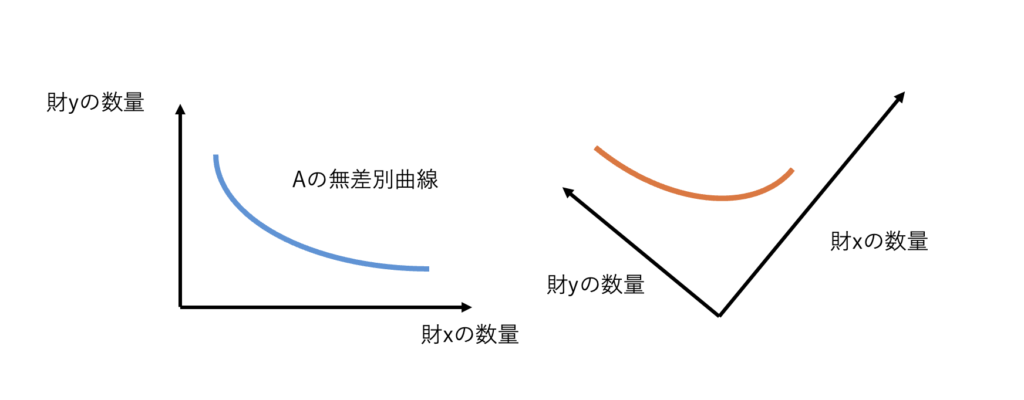
こうして、Bの方のグラフを反時計まわりに回転させて、
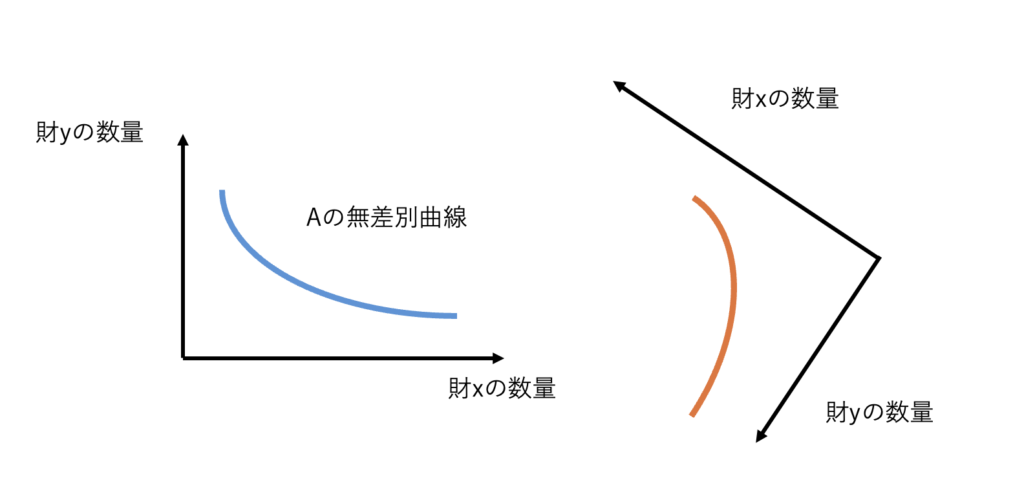
もう少し回転して、
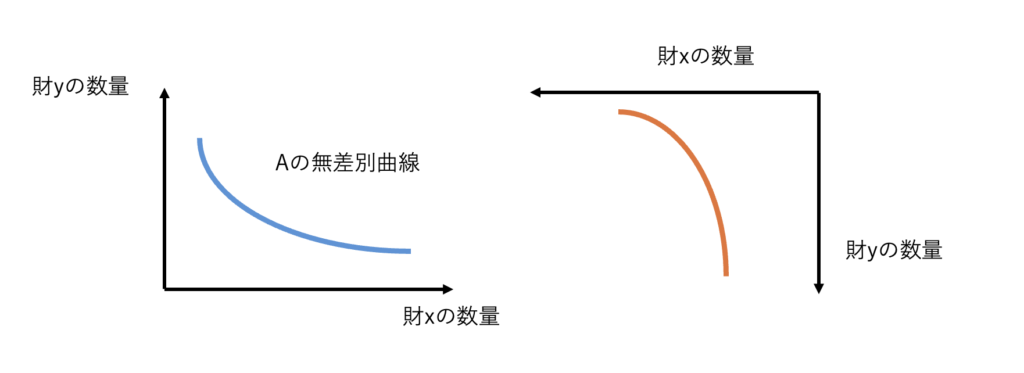
一旦この状態にします。そして、最後に、
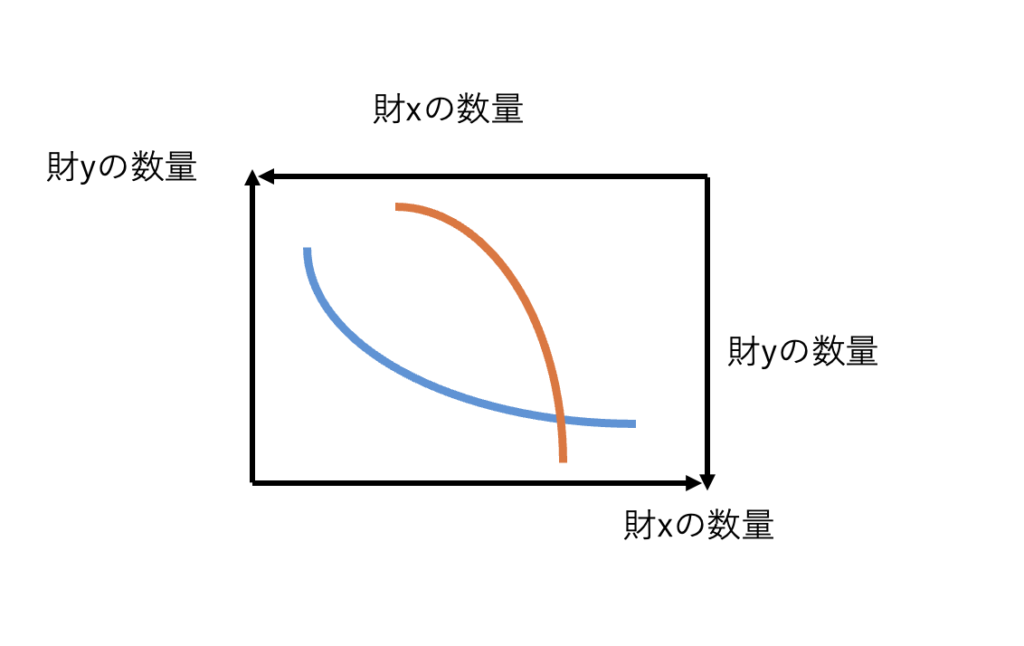
合体させます!!!!!!
このboxの横幅を\(q_x\)とし、縦幅を\(q_y\)とします。
すると、このboxの中で適当に1点とると、\(q_x^A, q_x^B, q_y^A, q_y^B\)を以下のように視覚化することができます。
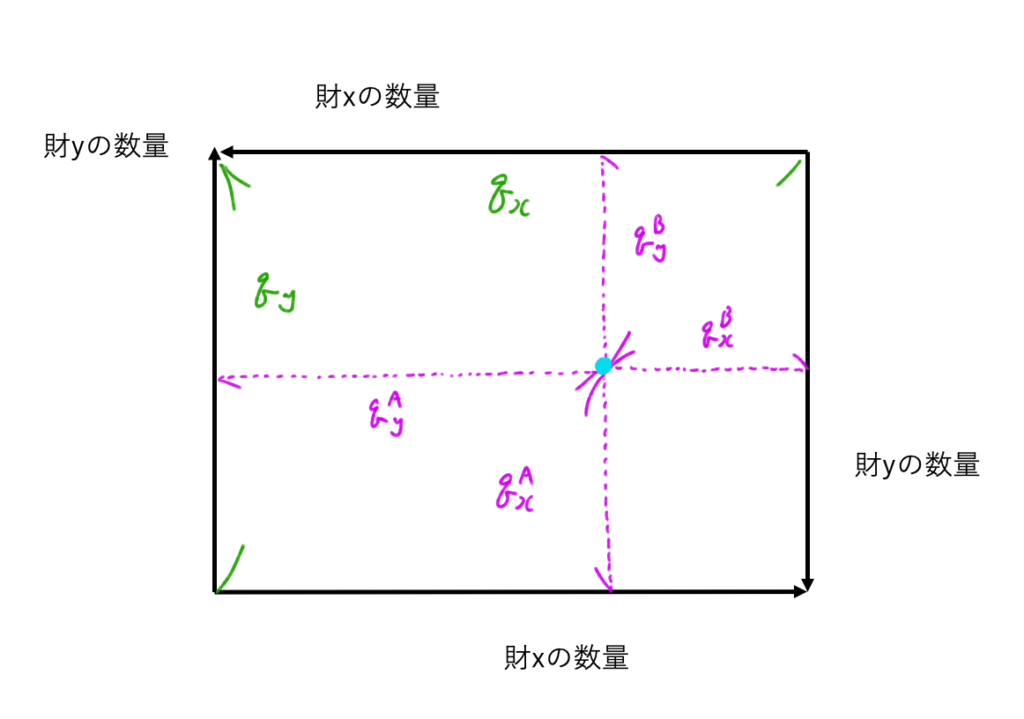
エッジワースボックスによるパレート最適の視覚化
パレート最適な点とは、一人が財を少しでも減らすことなく、他の人の効用を向上させることができない点です。
言い換えると、ある一人の効用を増加させようとすると、どうしても他の人の効用を減少させてしまう点です。
A, Bともにできるだけ高い効用を実現できるような無差別曲線を探索します。すると、
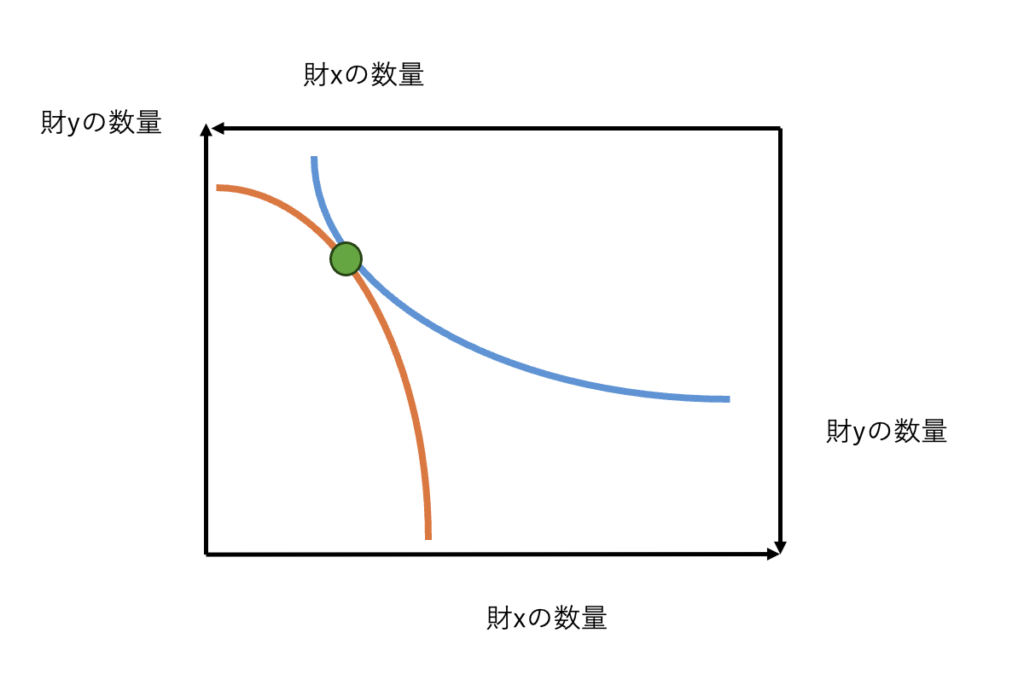
たとえばこのような状態では、緑の点はパレート最適な点になります。
なぜなら、A,Bともに、自分の効用を真に増加させるには、相手の効用を減らすようは配分にせざるを得ないからです。
(補足)このような点は違いの無差別曲線が接しているので、お互いに財の限界代替率が一致しています。
一方で、下の図でパレート最適でない点(図では緑点)を確認してみましょう。適当な効用の水準の無差別曲線を描画します。
青色がAの無差別曲線で、オレンジ色がBの無差別曲線であることをリマインドしておきます。
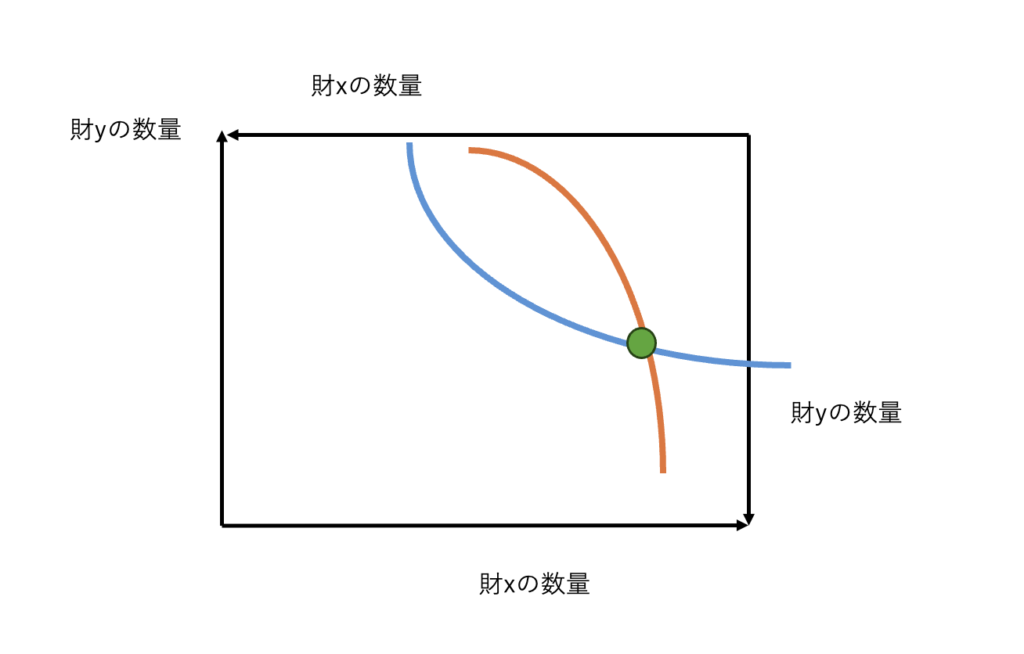
なぜなら、この緑の点よりも、
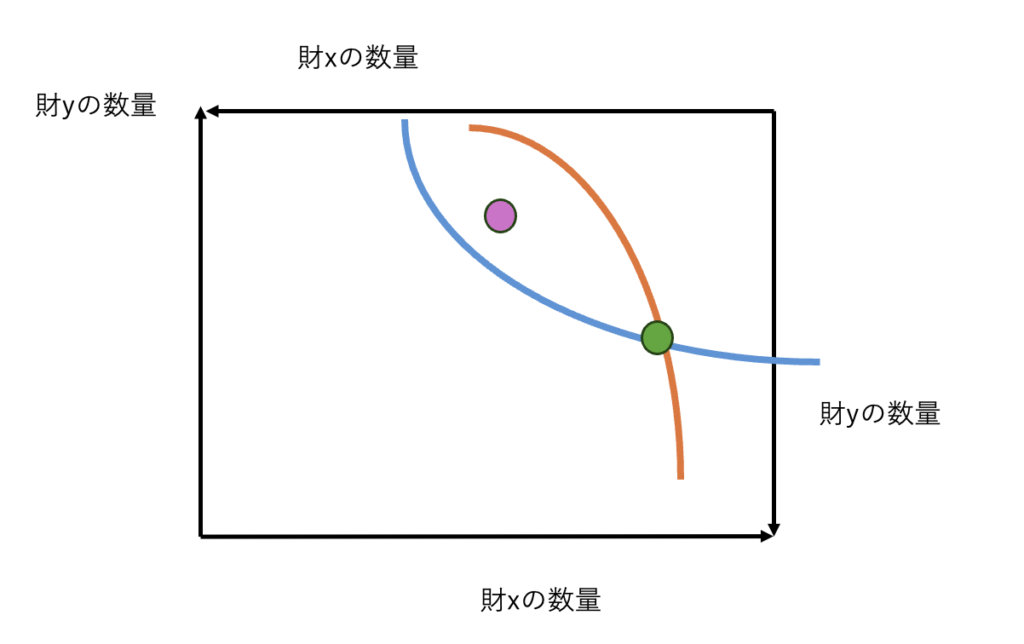
上図に描画されるようなピンクの点の財の配分の方が、AにとってもBにとっても、効用が真に大きいからです。
エッジワースボックスにおける契約曲線
図ではこのようなパレート最適な点を1点だけ探してきましたが、
パレート最適な点は他にもたくさん存在します。
例えば、(ごく自然な状況設定では)、Aが財を何も手にせず、Bが全ての財を手に入れているような状態です。
なぜなら、Aが自分の効用を真に増加させるためにBから財を少しいただこうとすると、Bの効用を減少させることになります。
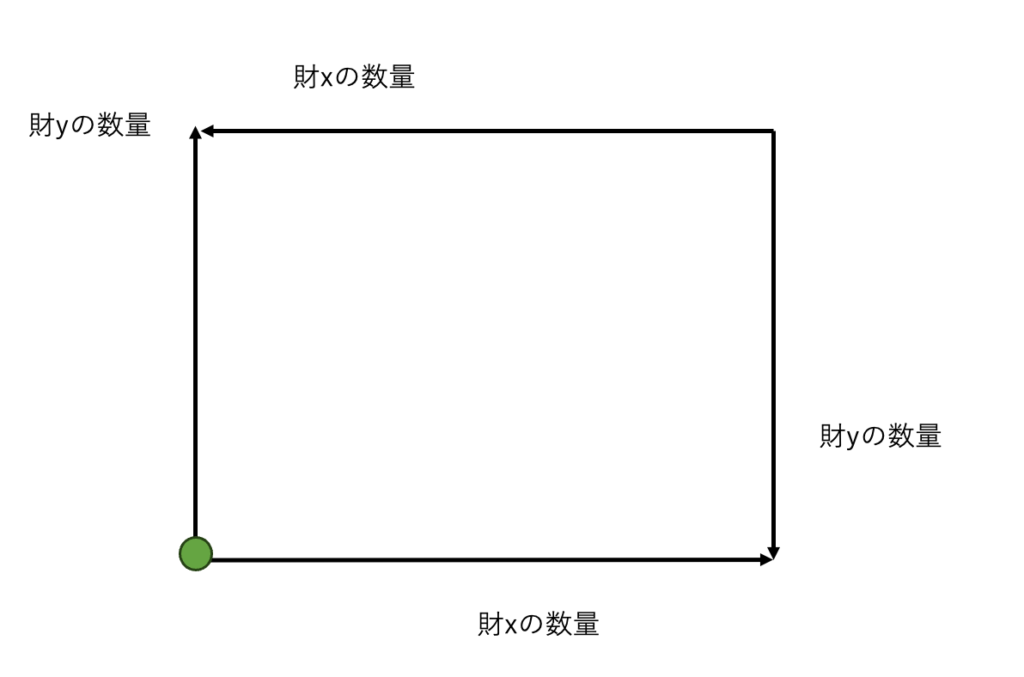
また似たような状況ですが、
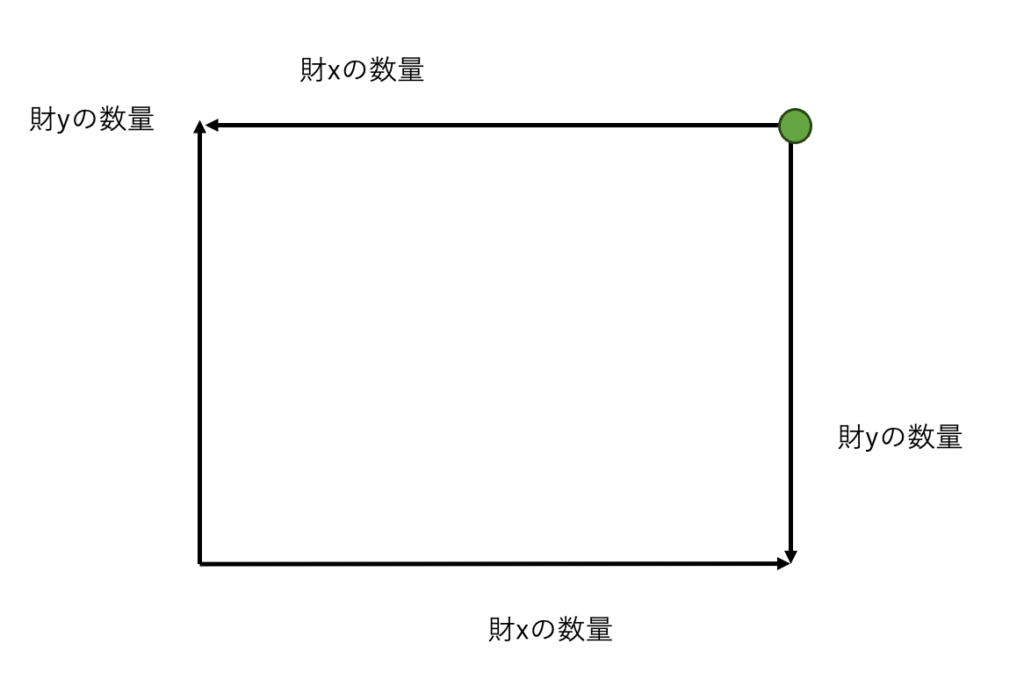
上図の緑点もパレート最適な点です。
これは、先ほどとは逆でBが財を何も手にせず、Aが全ての財を手に入れているような状態です。
なぜなら、Bが自分の効用を真に増加させるためにAから財を少しいただこうとすると、Aの効用を減少させることになるからです。
パレート最適な点を全て探し出して集めてきた点の集合を契約曲線と呼びます。
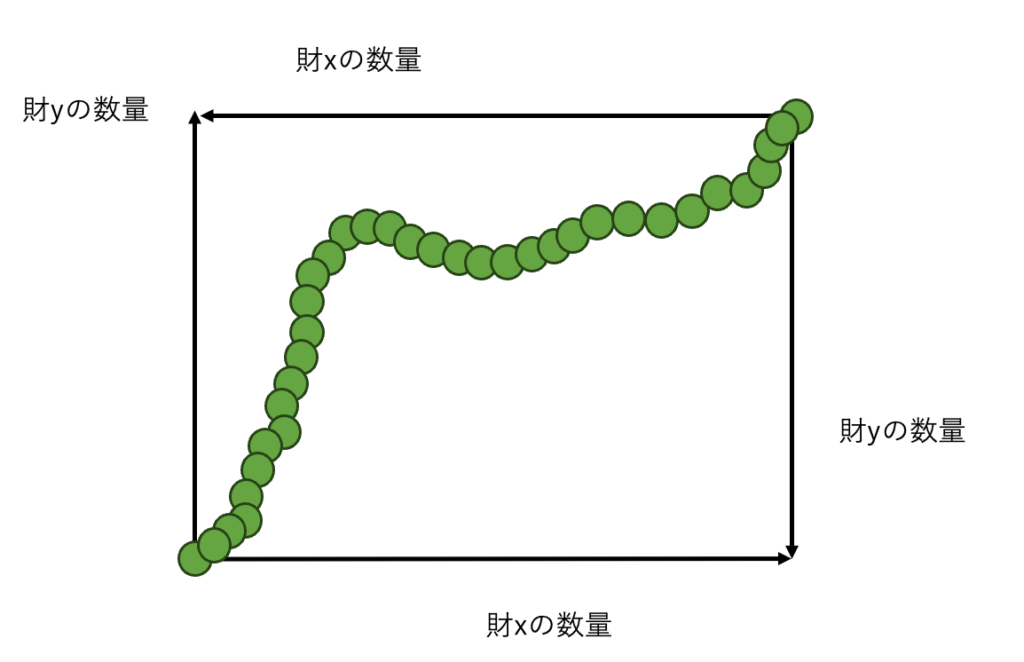
上の図における緑の点の集まりが契約曲線です。
エッジワースボックスにおけるコア配分
初期賦存が定められており、そこから財の交換を行う状況を考えてみましょう。
初期賦存とは、交換開始前の財の配分のことです。
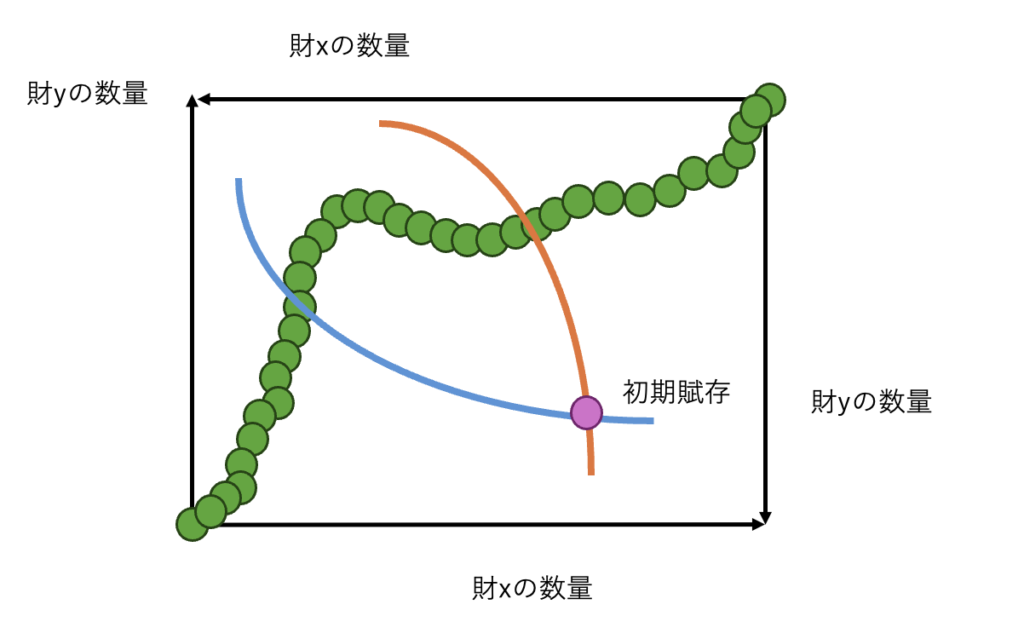
また、A, Bそれぞれの、初期賦存を通過する無差別曲線を描画しておきましょう。
このとき、交換によって自然に実現可能な配分はどこでしょうか。
もちろん、突然偉い人がやってきて「Aの財は全てBのものとする!」というかもしれませんが、
そういうのはナシで、
AもBも自分の効用が下がらないなら交換に合意することにします。
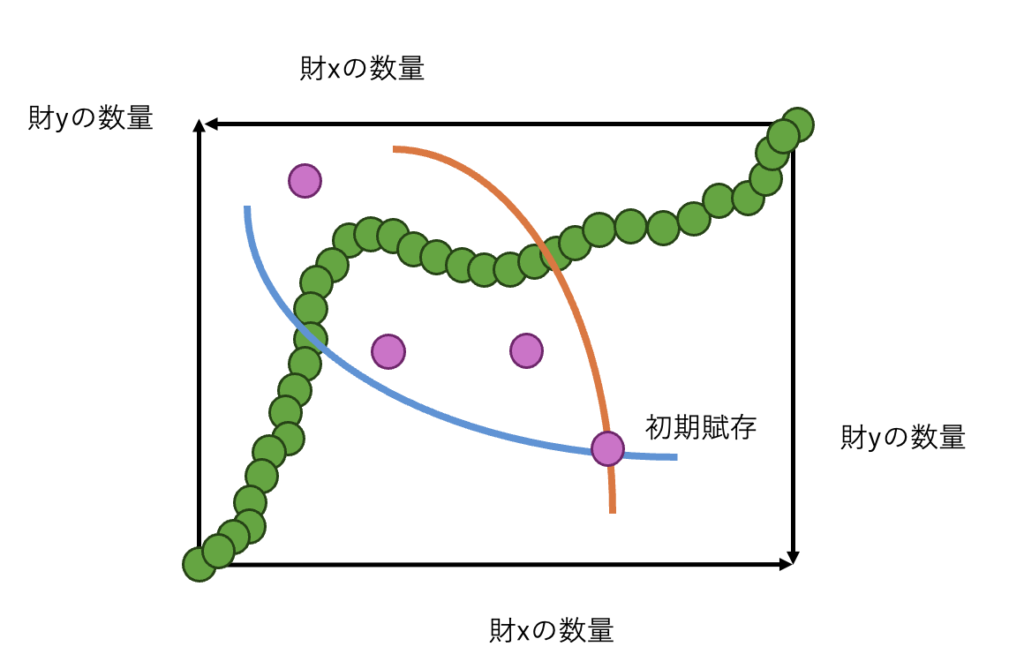
上の図中の、ピンクの点はどれも、誰も最初と比べて効用が下がらない点なので、実現可能な配分ということになります。
このような実現可能な配分のうち、最も良さげな点はどこでしょうか。
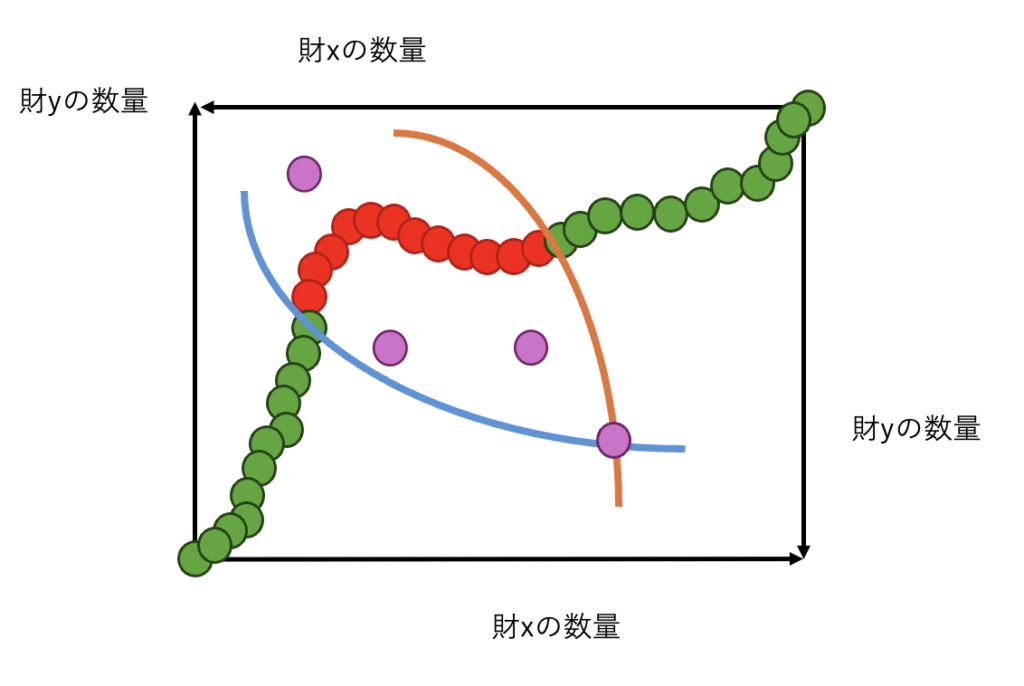
パレート最適であることを良い配分の基準とするならばそれは、図中の赤点の集合です。
このような赤点の集合をコア配分といいます。
初期賦存から実現可能な配分のうち、パレート最適な配分を、コア配分という。
ただし、ここで注意しておきたいことは、
コア配分は初期賦存に依存して決定されるため、
初期賦存が異なれば、コア配分も異なる。
ということです。
いかがでしたでしょうか。このようにエッジワースボックスは、経済学において、効率的な資源配分や社会的厚生に関する議論に役立ちます。
おすすめの参考図書











コメント