エクセルのソルバー機能を使用して線形計画問題(Linear Problem)を解く方法について説明します。線形計画問題は、限られたリソースを最適に配分し、行動を最適化するための強力なツールです。そして、エクセルのソルバー機能を使えば、これらの問題を簡単に解くことができます。自分のビジネスや日常生活において線形計画問題を適用できる場面を見つけ、エクセルで問題をモデリングし、最適な解を見つけてみましょう。
エクセルのソルバーで線形計画問題を解く方法をわかりやすく解説
線形計画問題とは
線形計画問題は、特定のリソースの制約下で、目的関数を最適化する数学的な方法を指します。この問題は、製造業、物流、金融、エネルギーなど、あらゆる業界で登場します。
具体的には、利益を最大化したり、コストを最小化したりするために、特定のリソースをどのように配分するべきかを決定する問題です。
線形計画問題を設計
線形計画問題を設計する際には、以下の三つの要素を明確に定義する必要があります。
- 目的関数: 最大化または最小化したい数量。例えば、利益の最大化やコストの最小化など。
- 決定変数: 目標関数の値に影響を与える変数。例えば、製造する商品の数量など。
- 制約条件: 決定変数の範囲を制限する条件。例えば、利用可能なリソースの上限や、必要な最小限の生産量など。
具体例に基づき線形計画問題を解く
それでは具体例とともにやり方を解説します。
- 彫刻職人: 彫刻職人のグループには、大師匠、師匠、弟子の3人がいます。
- 製品: 彫刻職人たちは、犬と猫の二つの種類の彫刻を作成して販売します。
- 利益: 犬の彫刻一個あたりの利益は15万円、猫の彫刻一個あたりの利益は17万円です。
- 作業時間:
- 犬の彫刻を一個作るのに、大師匠が1時間、師匠が2時間、弟子が4時間必要で、合計7時間かかります。
- 猫の彫刻を一個作るのに、大師匠が2時間、師匠が2時間、弟子が3時間必要で、合計7時間かかります。
- 労働時間の制約:
- 大師匠は1日に最大8時間までしか働けません。
- 師匠は1日に最大10時間までしか働けません。
- 弟子は1日に最大22時間まで働けます。
以上の情報を元に、線形計画問題を設計し、どの彫刻をどれだけ作るべきかを決定することが目標となります。これにより、彫刻職人たちの労働時間を最適に配分し、利益を最大化することが可能になります。
STEP1:線形計画問題を設計する
この問題を数式で表現します。
犬の彫刻の数量を\(x\)個とし、猫の彫刻の数量を\(y\)個とします。
すると、考えたい目的関数は
\begin{align*} 15 x + 17 y\end{align*}
となります。そして、制約条件は
(1)大師匠の労働時間
\begin{align*} x + 2y \leq 8 \end{align*}
(2)師匠の労働時間
\begin{align*} 2x + 2y \leq 10 \end{align*}
(3)弟子の労働時間
\begin{align*} 4x + 3y \leq 22 \end{align*}
となります。
改めてこの問題を整理すると、
\begin{align*} \textrm{maximize} \quad 15 x + 17 y \end{align*}
\begin{align*} \textrm{subject to}\begin{cases}x + 2y \leq 8 \\2x + 2y \leq 10 \\4x + 3y \leq 22 \end{cases} \end{align*}
となります。
STEP2:エクセルで線形計画問題をモデリングする
線形計画問題をエクセルに記述するためには、以下の手順に従います。
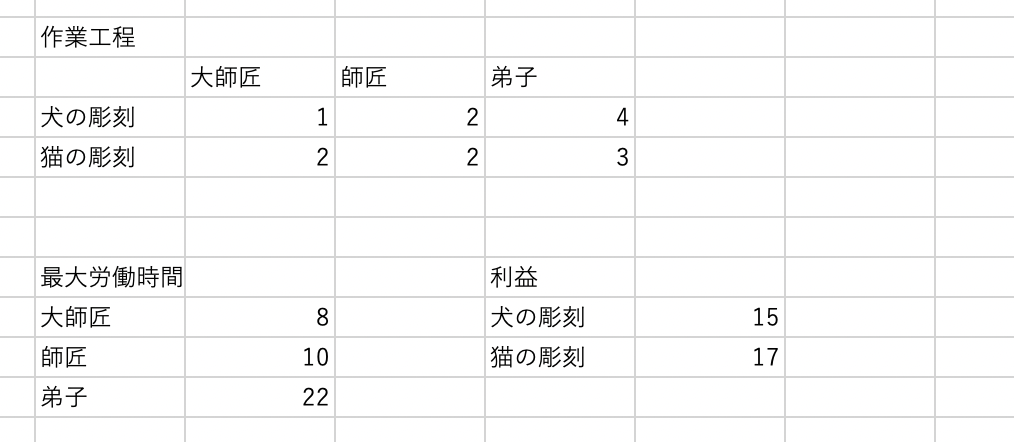
まずはこのように、決定変数以外の情報を記述します。次に、決定変数を設定します。
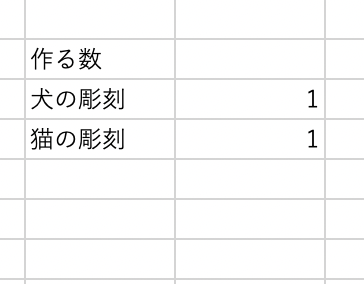
このとき、犬の彫刻の数量と猫の彫刻の数量は\(x, \quad y\) として、便宜的に、
\begin{align*} 1 \end{align*}
と記述しておきます。続いて、三人のそれぞれの実際の労働時間を計算するセルを用意します。
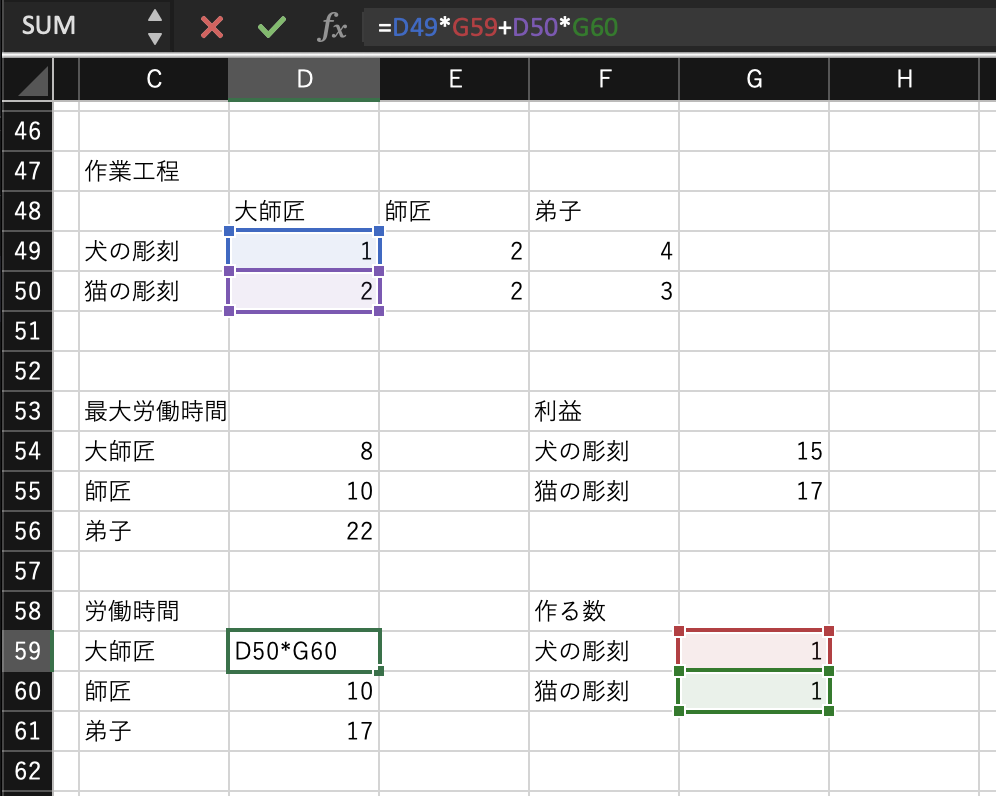
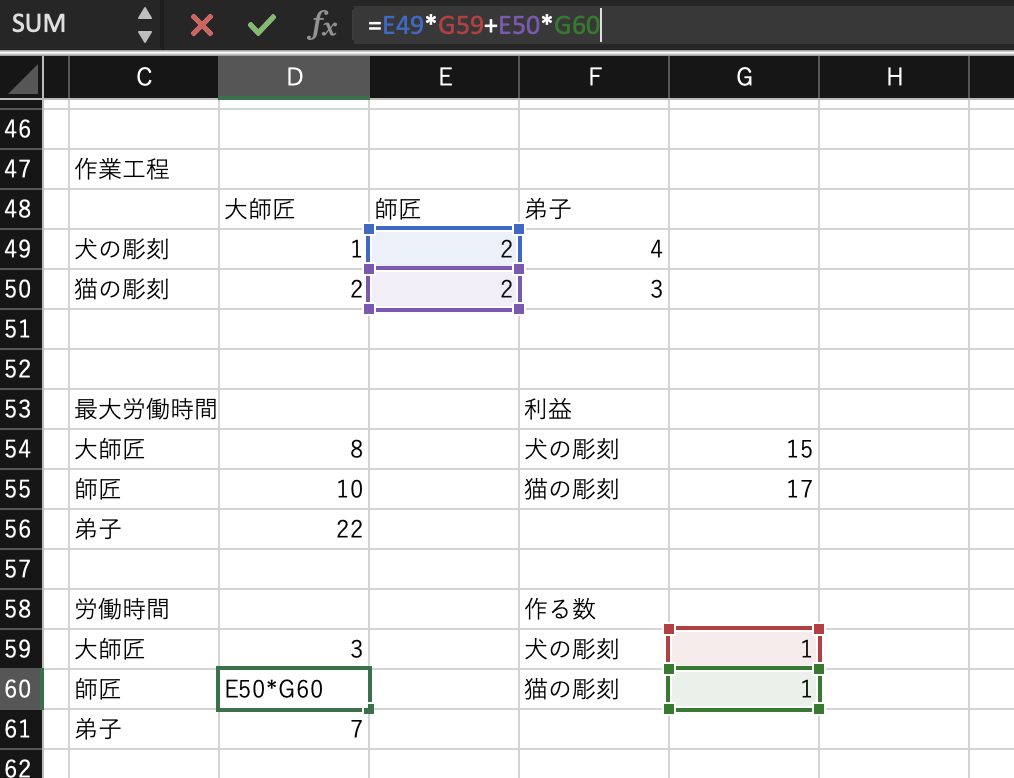
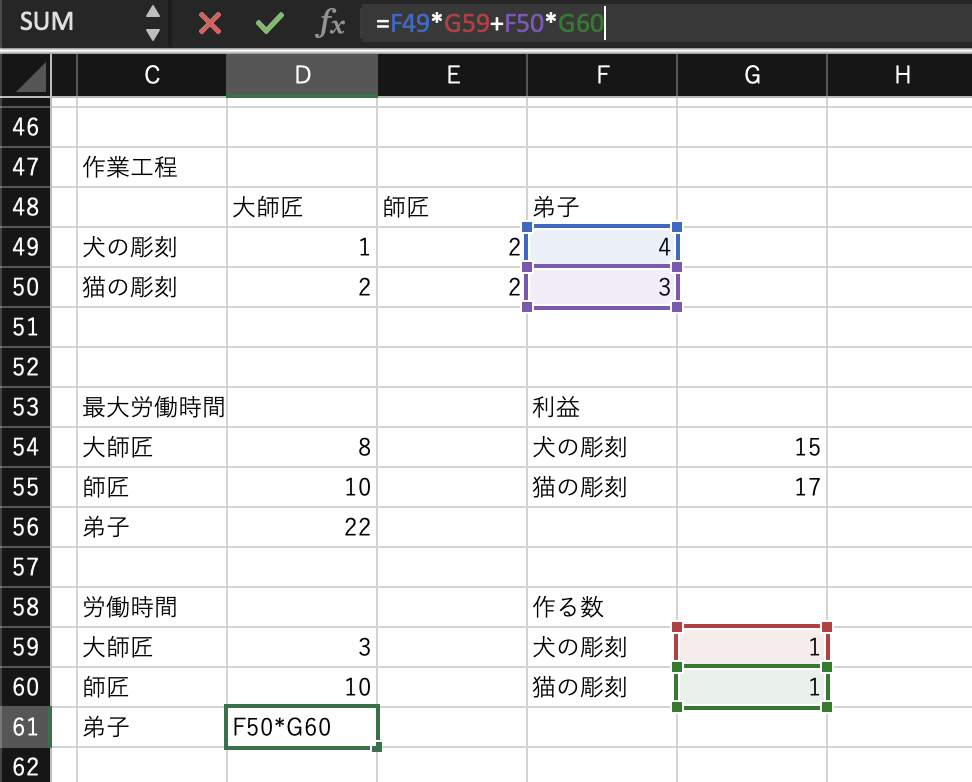
すると、仮想的に犬の彫刻と猫の彫刻を1個ずつ作った時の三人のそれぞれの労働時間が表示されるはずです。
そして、目的関数を設定するセルを準備します。
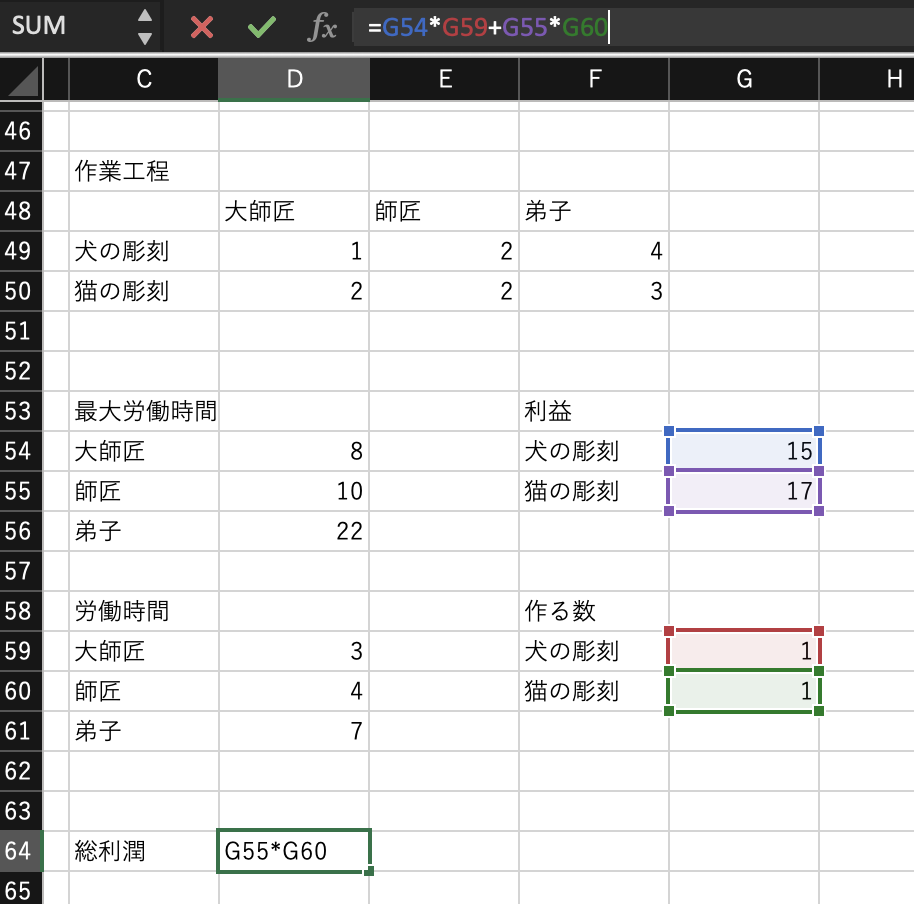
これで、セルに入力する段階を終えることができます。
STEP3:エクセルのソルバーを開く
ソルバーはエクセルの「データ」タブ→「ソルバー」にあります。
- ソルバーが見当たらない場合
-
・お使いのエクセルのバージョンによるかもしれません。ソルバーはエクセルの一部のバージョンにはデフォルトで含まれていますが、一部のバージョンでは別途アドインとして追加する必要があります。
・オンライン版のエクセル（Office 365やMicrosoft 365のブラウザ版）では、ソルバーのような一部の高度な機能が利用できないことがあります。
・Google スプレッドシートは、ソルバーのような線形計画法を解く機能は恐らく提供していません。もしかするとアップデートにより機能追加されている可能性もありますが。
STEP4:ソルバーの設定をする
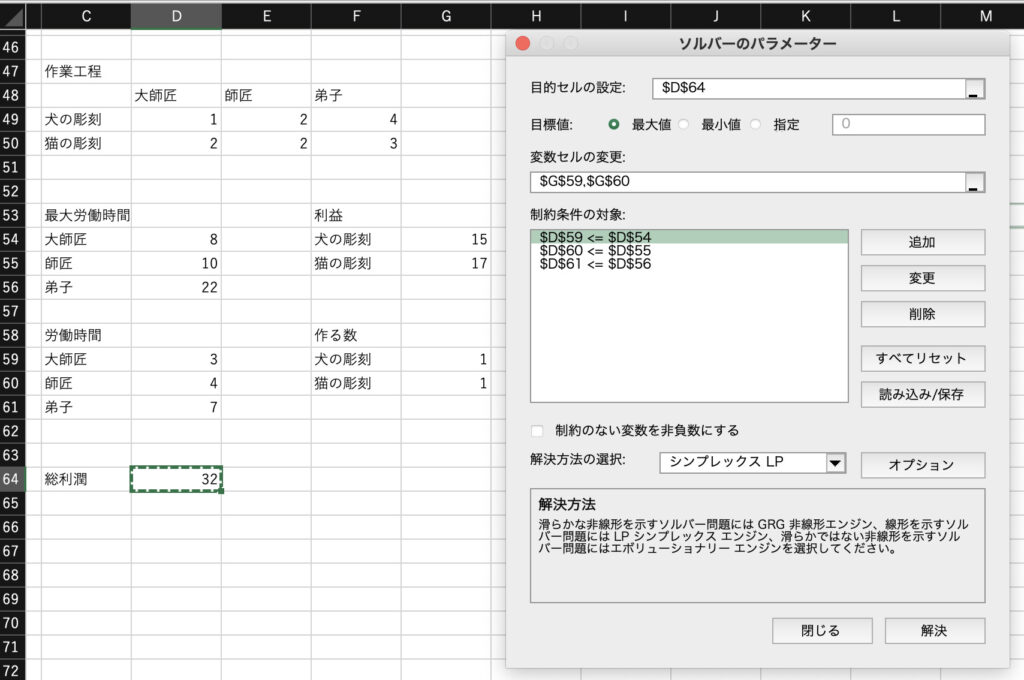
- (1)目的セルの設定
-
ここに、最適化したいセルを入力します。今回は総利潤を最適化したいので、「D64」を選択します。
- (2)目標値
-
目的関数「最大化」したいならば「最大値」を、「最小化」したいならば「最小値」にチェックをいれます。
今回は、目的関数(総利潤)を「最大化」したいので、「最大値」にチェックを入れます。
- (3)変数セルの変更
-
ここに、決定変数のセルを入力します。つまり、結局犬の彫刻と猫の彫刻をそれぞれ何個作るかを記述しているセル（先ほど便宜上ともに「1」に設定していたセル）なので、「G59」と「G60」を選択します。ソルバーを実行することにより、ここの値が変化します。
- (4)制約条件の対象
-
制約条件は、大師匠・師匠・弟子の労働時間についてでした。例えば「大師匠の労働時間は8時間以下」という条件をソルバーに設定するために、「追加」を選択して、「セルの参照」に大師匠の労働時間「D59」を、「制約条件」に大師匠の最大労働時間「D54」（つまり、「8」と入力されているセルです）を記述します。
師匠と弟子についての制約条件も同様に設定します。
- (5)解決方法の選択
-
「GRG非線形」や「シンプレックスLP」がありますが、線形計画問題なので「シンプレックスLP」を選んでおきます。
GRG非線形とシンプレックスLPは、最適化問題を解くための異なるアルゴリズムです。問題が線形か非線形かに応じて使い分けます。
シンプレックスLP（Linear Programming）: シンプレックス法は、線形計画問題を解くためのアルゴリズムです。つまり、目標関数および制約条件がともに線形（一次）である問題に対して適用されます。
GRG（Generalized Reduced Gradient）非線形: GRG非線形ソルバーは、非線形計画問題を解くためのアルゴリズムです。目標関数や制約条件が非線形（つまり、2次以上の多項式や指数関数、対数関数など）で表される場合に使用されます。
これらを設定し終えたら、
\begin{align*} \textrm{「解決」}\end{align*}
を押します。
STEP5:ソルバーによる結果をみる
解決を押すと、何事も問題がなければ
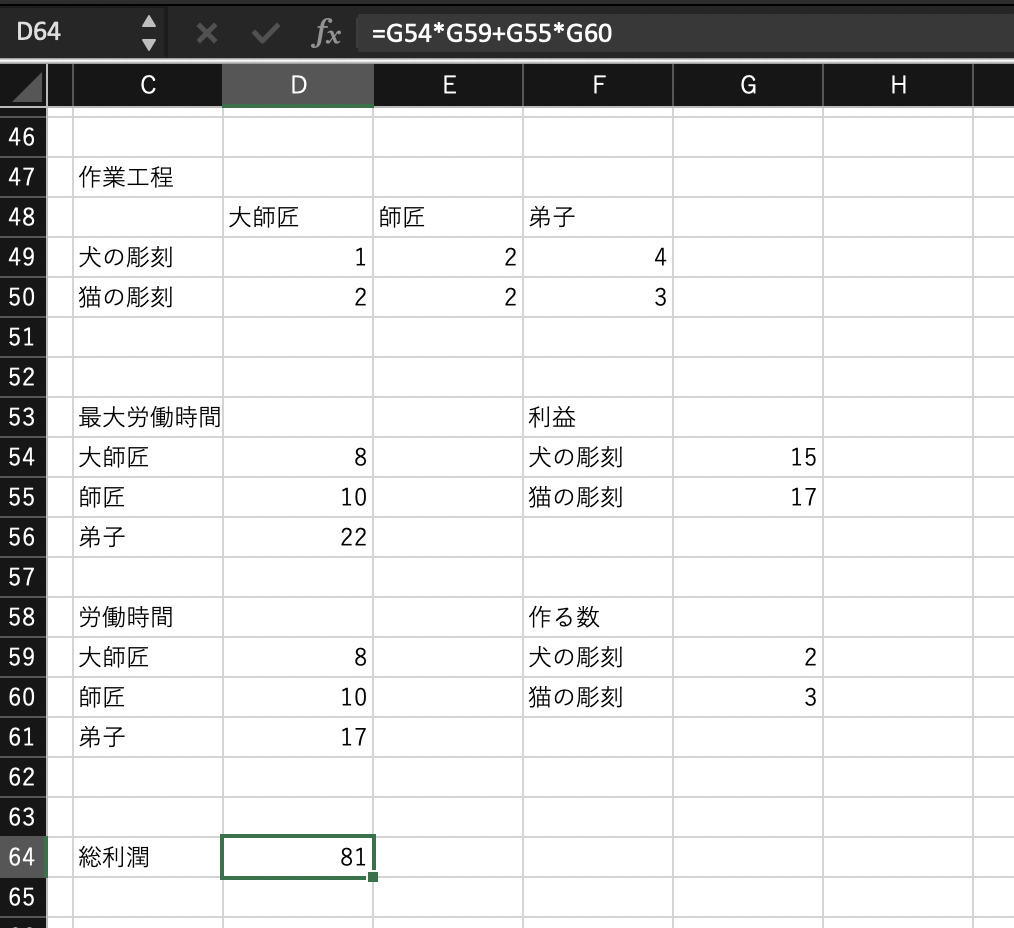
このように、線形計画問題を解いた結果がセルに反映されます。
実際、犬の彫刻と猫の彫刻の作る数のセルが「2」と「3」に変化しており、それに応じて労働時間が変化し、さらに総利潤が「81」に変化していることが確認できると思います。
犬の彫刻を2個、猫の彫刻を3個作った場合が利潤を最大化できる場合である。
その利潤は81万円である。
もともと、弟子は1日最大で22時間まで働くことが可能な体制でした。しかし、大師匠と師匠の最大労働時間という制約があるおかげで、弟子は実際には17時間しか働く必要がないことが明らかになりました。よかったです。
今回の記事では、エクセルのソルバーを使用して線形計画問題を解く方法について解説しました。
具体的に、彫刻職人のグループが彫刻を作り、それを販売して利益を最大化するという状況を考えました。それぞれの彫刻にかかる時間と各職人の最大労働時間という制約の中で、どのように作業を分配すべきかを調査しました。線形計画問題を数式で表現し、エクセルのソルバーにそれを適用することで、利益を最大化しつつ各職人の労働時間を最適に配分する解法を導き出しました。
エクセルのソルバーは、このように実際のビジネス問題を解決するための強力なツールであり、適切な方法で使用すれば、働く時間の配分からリソースの最適化まで、さまざまな課題に対する洞察を提供します。
あわせて読みたい記事
コメント