みなさん、こんにちは!統計学や確率論に慣れ親しんでいる方なら、正規分布について何度も聞いたことがあることでしょう。正規分布は、自然界や社会科学など、さまざまな分野で出現する現象をモデル化するのに非常に役立ちます。今日は、このおなじみの正規分布に、ちょっと変わった視点で迫ってみたいと思います。
具体的には、確率変数 \(X\) が平均\(\mu\)分散\(\sigma^2\) の正規分布に従うとき、すなわち \(X \sim \mathcal{N}(\mu, \sigma^2)\) であるとき、その指数関数 \(Y = e^X\) が従う分布を対数正規分布と言います。
対数正規分布の確率密度関数と期待値と分散を導出してみようと思います。
対数正規分布の確率密度関数・期待値・分散の導出
対数正規分布の確率密度関数の導出
\(e^X\) の密度関数を\(f(x) \) と書くことにします。\(f(x) = \partial_x P(X \leq x)\) が成り立つことを思い出しておきます。
\begin{align*} P(X \leq x) = \int_{-\infty}^{x} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(s- \mu)^2}{2 \sigma^2}} ds\end{align*}
であるので、\(x > 0\) の時には、
\begin{align*} P(e^X \leq x) = P(X \leq \log x) = \int_{-\infty}^{\log x} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(s- \mu)^2}{2 \sigma^2}} ds\end{align*}
です。
\begin{align*} \partial_x \int_{-\infty}^{b(x)} f(t) dt = b^\prime (x) f(b(x)) \end{align*}
であることを思い出すと、
\begin{align*} f(x) = \partial_x P(e^X \leq x) = \frac{1}{x} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(\log x- \mu)^2}{2 \sigma^2}} \end{align*}
となります。
従って、まとめると、
\begin{align*} f(x) = \begin{cases} \frac{1}{x} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(\log x- \mu)^2}{2 \sigma^2}} &(x > 0) \\ 0 & (x \geq 0) \end{cases} \end{align*}
ということになります。
対数正規分布の期待値の求め方
ガウス関数の積分
\begin{align*} \int_{-\infty}^\infty \frac{1}{2 \pi t} e^{- \frac{x^2}{2t}} dx = 1 \end{align*}
を思い出しておく。
\begin{align*} E(e^X) &= \int_{-\infty}^{\infty} e^x \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x- \mu)^2}{2 \sigma^2}} dx \\&= \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x^2 – (2 \mu + 2 \sigma ^2) x + \mu ^2 )}{2 \sigma^2}} dx \\&= \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x – (\mu + \sigma^2) ) ^2 – (2 \mu \sigma^2 + \sigma^4) }{2 \sigma^2}} dx \\&= e^{ \mu + \frac{1}{2} \sigma^2} \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x- (\mu + \sigma^2))^2}{2 \sigma^2}} dx \\&= e^{ \mu + \frac{1}{2} \sigma^2} \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{x^2}{2 \sigma^2}} dx \\&= e^{ \mu + \frac{1}{2} \sigma^2} \times 1 \\ &= e^{ \mu + \frac{1}{2} \sigma^2} \end{align*}
まとめると、確率変数 \(X\) が平均\(\mu\)分散\(\sigma^2\) の正規分布に従うとき、\(Y = e^X\) とすると、
\begin{align*} E(Y) = e^{ \mu + \frac{1}{2} \sigma^2} \end{align*}
となります。
対数正規分布の分散の求め方
\(V(Y) = E(Y^2 ) – (E(Y))^2 = E(e^{2X}) – (E(e^X))^2\) が成り立つことを用いることにします。
\begin{align*} E(e^{2X}) &= \int_{-\infty}^{\infty} e^{2x} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x- \mu)^2}{2 \sigma^2}} dx \\&= \int_{-\infty}^\infty \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x^2 – (2 \mu + 4 \sigma ^2) x + \mu ^2 )}{2 \sigma^2}} dx \\&= \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x – (\mu + 2\sigma^2) ) ^2 – (4 \mu \sigma^2 + 4\sigma^4) }{2 \sigma^2}} dx \\&= e^{2\mu + 2\sigma^2} \int_{-\infty}^{\infty} \frac{1}{(2 \pi \sigma^2)^{1/2}} e^{- \frac{(x – (\mu + 2\sigma^2) ) ^2 }{2 \sigma^2}} dx \\&= e^{2\mu + 2\sigma^2} \end{align*}
また、
\begin{align*} (E(e^X))^2 = e^{2 \mu + \sigma ^2 }\end{align*}
なので、
\begin{align*} V(Y) = e^{2\mu + 2\sigma^2} – e^{2 \mu + \sigma ^2 } \end{align*}
となります。
おまけ:連続複利が対数正規分布に従う場合
連続複利が正規分布に従っているとします。つまり、\(r \sim \mathcal N(\mu, \sigma^2) \) です。
\(1\) 円を1年間運用すると、\(e^r\) になります。このときのリターン\(\frac{e^{r} -1}{1} \)を\(R \) と表すことにすると、
期待値は、
\begin{align*} E(R) = E(e^r -1 ) = e^{ \mu + \frac{1}{2} \sigma^2} – 1 \end{align*}
と計算できます。また分散については、
\begin{align*} V(R) = V(e^r -1 ) = V(e^r) = e^{2\mu + 2\sigma^2} – e^{2 \mu + \sigma ^2 } \end{align*}
と計算することができます。
おまけ2:確率密度関数を実際にみてみよう
確率変数 \(X\) が平均\(\mu\)分散\(\sigma^2\) の正規分布に従うとします。
\(Y = e^X\) の密度関数の分布をみてみましょう。
\(\sigma = 0.2\) に固定して、\(\mu\) を変化させたとき以下のようになります。
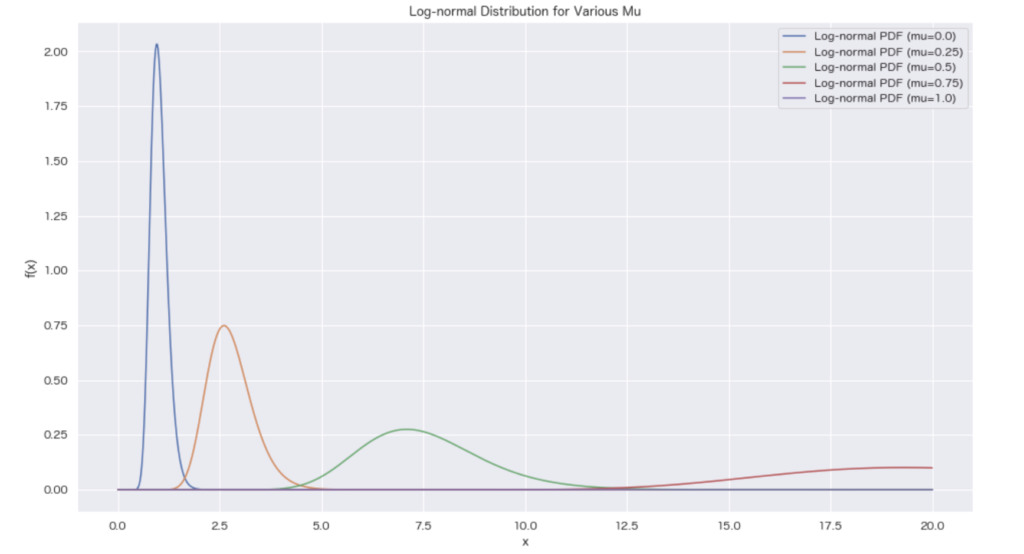
import numpy as np
import matplotlib.pyplot as plt
# フィギュアのサイズを設定
plt.figure(figsize=(16, 9))
# 対数の標準偏差
sigma = 0.2
# xの値の範囲
x = np.linspace(0.01, 20, 1000)
# 対数の期待値muの値を0, 1/4, 2/4, 3/4, 1と変化させる
mu_values = np.linspace(0, 4, 5)
# 各mu値に対して対数正規分布の密度関数をプロット
for mu in mu_values:
# 対数正規分布の密度関数
pdf = (1 / (x * sigma * np.sqrt(2 * np.pi))) * np.exp(-((np.log(x) - mu) ** 2) / (2 * sigma ** 2))
# 密度関数をプロットする
plt.plot(x, pdf, label=f'Log-normal PDF (mu={mu / 4})')
# グラフにタイトルとラベルを追加
plt.title('Log-normal Distribution for Various Mu')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
# グラフを表示
plt.show()
また、\(\mu\) を\(0\)に固定して、\(\sigma\) を動かしたときの様子は以下のようになります。
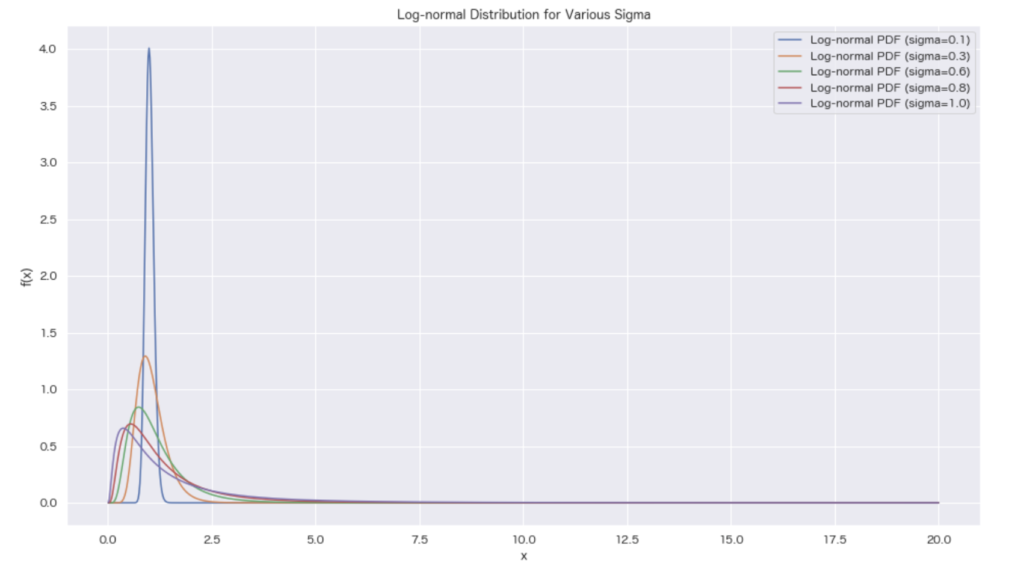
import numpy as np
import matplotlib.pyplot as plt
# フィギュアのサイズを設定
plt.figure(figsize=(16, 9))
# 平均の対数
mu = 0.0
# xの値の範囲
x = np.linspace(0.01, 20, 1000)
# sigmaの値を0.1, 0.3, 0.6, 0.8, 1.0と変化させる
sigma_values = np.linspace(0.1, 1, 5)
# 各sigma値に対して対数正規分布の密度関数をプロット
for sigma in sigma_values:
# 対数正規分布の密度関数
pdf = (1 / (x * sigma * np.sqrt(2 * np.pi))) * np.exp(-((np.log(x) - mu) ** 2) / (2 * sigma ** 2))
# 密度関数をプロットする
plt.plot(x, pdf, label=f'Log-normal PDF (sigma={sigma:.1f})')
# グラフにタイトルとラベルを追加
plt.title('Log-normal Distribution for Various Sigma')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
# グラフを表示
plt.show()あわせて読みたい記事

















コメント