限界代替率(MRS: Marginal Rate of Substitution)とは、経済学において消費者の選好を表現する重要な概念であり、特定の財の組み合わせにおいて、ある財を1単位追加で得るために、他の財をどれだけ犠牲にできるかを示します。
限界代替率の計算方法をわかりやすく解説!!
限界代替率とは、財xと財y という2つの異なる財の組み合わせにおいて、
財xを1単位追加した際に、もう一方の財yをどれだけ減らしても構わない(効用が同じ)かという消費者の意思を定量的に示すものです。
無差別曲線とは
無差別曲線とは、同じ効用水準を実現できる財の組み合わせの集合です。
数学的に正確な定義を提供するため、2つの財のみを考えるシンプルな状況を想定します。
財xと財yの数量をそれぞれ\(x\)および\(y\)としましょう。
ある個人が存在し、その人の効用関数を\(u\)で表すとします。
このとき、効用水準\(\overline{u} \in \mathbb{R}\)を達成する無差別曲線は以下のように表されます。
\begin{align*} \{(x, y) \mid u(x, y) = \overline u \}\end{align*}
つまり、無差別曲線とは、2変数関数\(u\)の特定の高さに対応する等高線です。
一般的に、無差別曲線は以下のような形状を持ちます。
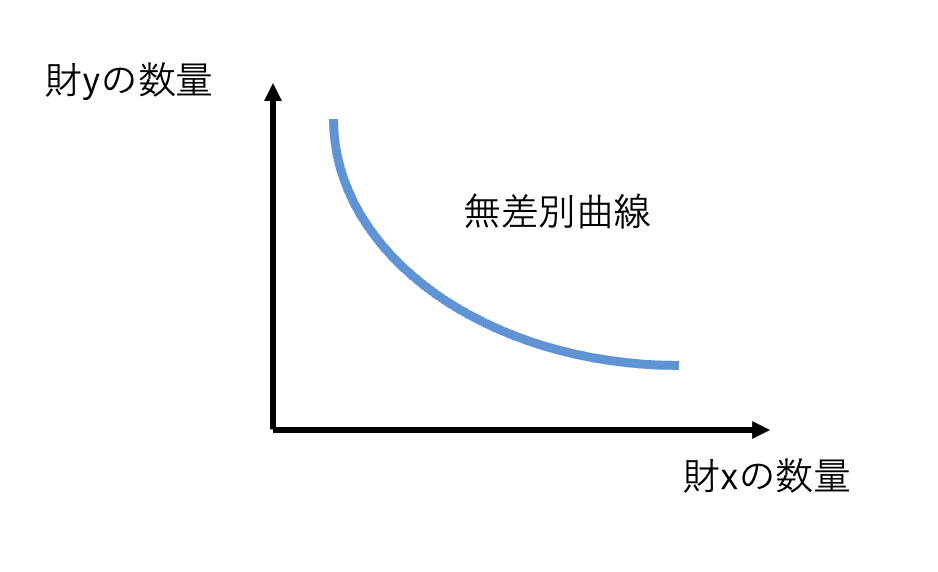
この青線の上の\(x, y\)の組み合わせであれば、効用は同じであるということです。
限界代替率とは
限界代替率は、財xを1単位追加した際に、もう一方の財yをどれだけ減らしても構わない(効用が同じ)かを表す値です。
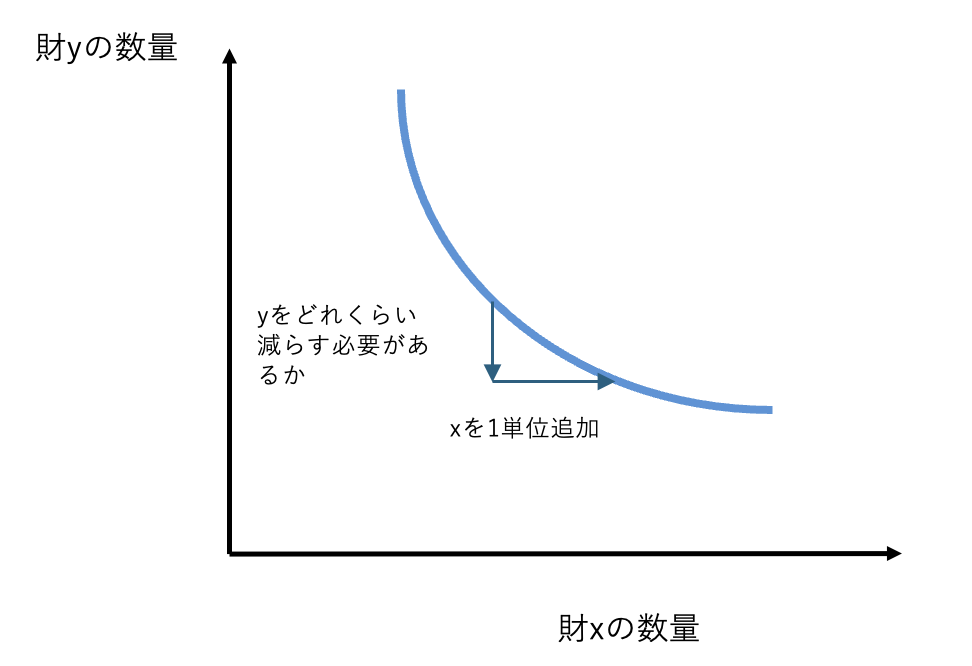
これを求めるには、つまるところ無差別曲線の接線の傾きを考えれば良いことがわかります。
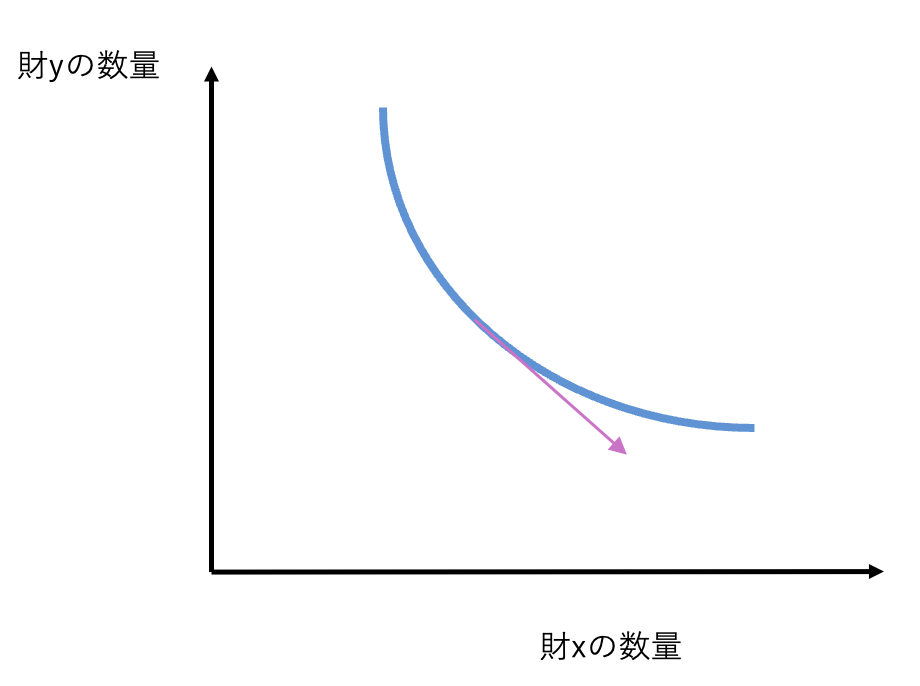
結論からいうと、傾きは、効用関数を\(u\)で表すことにすると、
\begin{align*} \frac{- \frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}}\end{align*}
です。
導出してみましょう!!!
無差別曲線が、効用\(\overline u\)を実現するものであるとしましょう。つまり、
\begin{align*} \{(x, y) \mid u(x,y) = \overline{u} \}\end{align*}
がこの無差別曲線です。ここで、この無差別曲線を
\begin{align*} t \mapsto (x(t), y(t))\end{align*}
とパラメータ付けします(ごく自然な状況ではこのようにパラメータ付け可能です)。
この曲線上で
\begin{align*} u(x(t),y(t)) = \overline u \end{align*}
であるので、両辺を\(t\)で微分すると、
\begin{align*} \frac{\partial u}{\partial x} \frac{dx}{dt} + \frac{\partial u }{\partial y} \frac{dy}{dt} = 0 \end{align*}
です。これは内積の表記に書き換えると、
\begin{align*} (\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}) \dot (\frac{dx}{dt}, \frac{dy}{dt}) = 0\end{align*}
と書くことができます!
よく考えるとこれは、無差別曲線の接ベクトル\((\frac{dx}{dt}, \frac{dy}{dt})\)と、\((\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y})\)が直交することを意味しています。
ということは、\((\frac{\partial u}{\partial x}, \frac{\partial u}{\partial y})\)を法線とし、点\((x_0, y_0)\)を通る直線が求める接線なので、その方程式は、
\begin{align*} \frac{\partial u}{\partial x}(x – x_0) + \frac{\partial u}{\partial y}(y – y_0) = 0\end{align*}
となります。これを、書き換えると、
\begin{align*} y = -\frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} x + \frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} x_0 + \frac{1}{\frac{\partial u}{\partial y}} y_0 \end{align*}
なので、傾きが
\begin{align*} -\frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} \end{align*}
ということがわかります。
効用関数を\(u\)とする。\((x_0, y_0)\)における限界代替率は、
\begin{align*} \rm{MRS}_x y := -\frac{\frac{\partial u}{\partial x}}{\frac{\partial u}{\partial y}} (x_0, y_0) \end{align*}
により定義される。
おすすめの参考図書











コメント