p乗可積分とq乗可積分ならばr乗可積分である条件を証明

2023年6月17日2023年7月19日

L^pかつL^qならばL^rとなる条件、(p乗可積分とq乗可積分ならばr乗可積分である条件)を証明します。これは、解析学や測度論における重要な結果であり、関数の性質を理解する上で基本的なツールとなっています。

L^p可積分性とL^q可積分性からL^r可積分性が従うか

まず、\(0 < p < r < q < \infty\) としましょう。また、関数\(f: \mathbb R^n \rightarrow \mathbb R\) を考えますが、この関数は\(L^p(\mathbb R^n)\) および \(L^q(\mathbb R^n)\)の両方に属しているとします。

目標は、この関数\(f\)が\(L^r(\mathbb R^n)\)にも属することを示すことです。つまり、\(f \in L^r(\mathbb R^n)\) が成り立つかを調べます。

事前準備

実数\(a > 0\) に関する重要な性質を振り返りましょう。それは、次のようになります。

\begin{align*} &0 \leq a \leq 1 \Rightarrow a^r \leq a^p \ &1 \leq a \Rightarrow a^r \leq a^q \end{align*}

これは、\(a\)が0以上1以下の場合、\(a^r\)は\(a^p\)以下であり、\(a\)が1以上の場合、\(a^r\)は\(a^q\)以下であることを意味します。

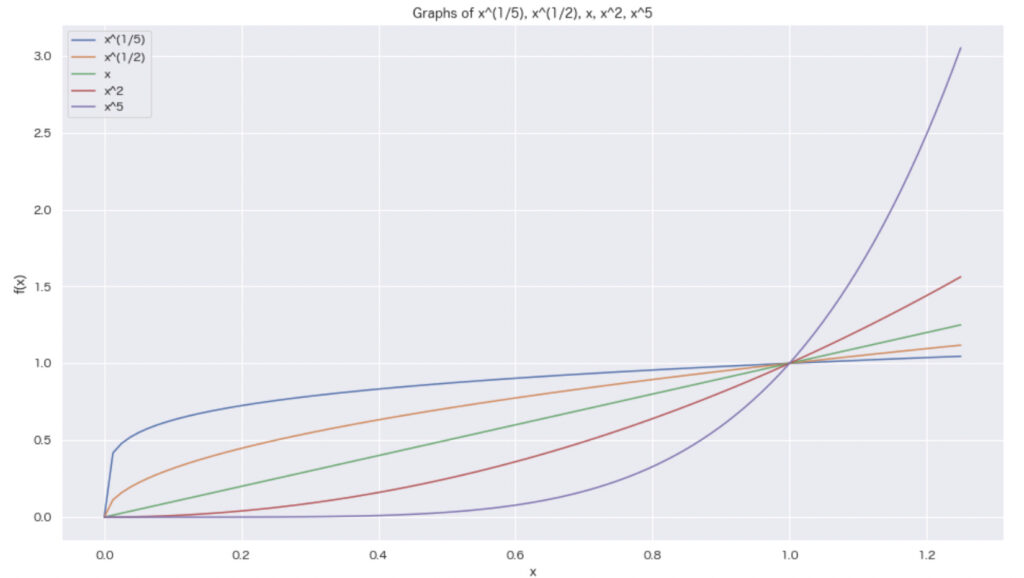
グラフにするとこんな感じです。

L^p可積分性とL^q可積分性からL^r可積分性が従うことの証明

これを踏まえて、

命題

\(0 < p < r < q < \infty\) とし、\(f: \mathbb R^n \rightarrow \mathbb R\) を\(f \in L^p(\mathbb R^n) \cap L^q(\mathbb R^n)\) とする。

このとき、\(f \in L^r(\mathbb R^n)\) が成り立つ。

という命題を証明してみましょう。

\(|f|^r\)の積分を考えます。

\begin{align*} \int_{\mathbb R^n} |f|^r dx &= \int_{\mathbb R^n} 1_{|f| \leq 1} |f|^r dx + \int_{\mathbb R^n} 1_{1 \leq |f|} |f|^r dx \\& \leq \int_{\mathbb R^n} 1_{|f| \leq 1} |f|^p dx + \int_{\mathbb R^n} 1_{1 \leq |f|} |f|^q dx \\& \leq \int_{\mathbb R^n} |f|^p dx + \int_{\mathbb R^n} |f|^q dx \end{align*}

この式が成り立つことから、\(f\)が\(L^r(\mathbb R^n)\)に属することが示されます。

L^1かつL^∞ならばL^2

全く同じストーリーで、例えば以下のことを証明できます。

命題

\(f \in L^1(\mathbb R^n) \cap L^\infty (\mathbb R^n)\)であるならば、\(1 \leq s \leq \infty\)に対して

\begin{align*} f \in L^s (\mathbb R^n) \end{align*}

が成り立つ。

実際、

\begin{align*} \int |f|^s dx &= \int_{\mathbb R^n} 1_{|f| \leq 1} |f|^2 dx + \int_{\mathbb R^n} 1_{1 \leq |f|} |f|^2 dx \\& \leq \int_{\mathbb R^n} 1_{|f| \leq 1} |f|^1 dx + ||f||_{\infty} dx \\& \leq \int_{\mathbb R^n} |f|^p dx + \int_{\mathbb R^n} |f|^q dx \end{align*}