無限級数∑1/(n^2-x) が収束するようなxの範囲

次の無限級数の収束を考えます。

\begin{align*} \sum_{n = 1}^\infty \frac{1}{n^2 – x} \end{align*}

この無限級数が収束する\(x\)の範囲を求めることが目的です。

無限級数∑1/(n^2-x) が収束するようなxの範囲

事前準備

まず、次の公式を思い出しておきましょう。

\begin{align*} \sum_{n = 1}^\infty \frac{1}{n^2} = \frac{\pi ^2}{6} \end{align*}

これは、$1$から無限までの自然数の二乗の逆数を足し合わせたときの和が$\frac{\pi ^2}{6}$になるという公式です。

解答

それでは、\(x\)の値によって場合分けをして考えてみましょう。

\(x < 0\) のときを考えます。

\begin{align*} n^2 – x > n^2 \end{align*}

が成り立つので、

\begin{align*} \frac{1}{n^2 – x} > \frac{1}{n^2} \end{align*}

となり、

\begin{align*} \sum_{n = 1}^\infty \frac{1}{n^2 – x} < \sum_{n = 1}^\infty \frac{1}{n^2} < \infty \end{align*}

となります。

一方で、 \(x \geq 0\) のときを考えます。まず、\(x = 1, 4, 9, \dots \) のように平方数の場合には\(n^2 – x = 0\) となるような自然数\(n \in \mathbb N\) があるので、 無限の値をとってしまいます。

\(x\) が平方数でないところを考えましょう。 \(x\) より大きい整数\(M\) を適当にひとつとります。

\(M + 1 \leq n\) の場合には

\begin{align*} n^2 – x &\geq n^2 – M \\&= (n – M + M ) ^2 – M \\&= (n-M)^2 + 2M(n-M) + (n – M)^2 – M \\& = (n- M)^2 + M(n + n – M) + (n – M)^2 \\& \geq (n- M)^2\end{align*}

という不等式を得ます。従って、

\begin{align*} \sum_{n = 1}^\infty \frac{1}{n^2 – x} = \sum_{n = 1}^M \frac{1}{n^2 – x} + \sum_{n = M +1}^\infty \frac{1}{n^2 – x} \end{align*}

とわけると、右辺の第1項は有限和なので、有限の値をとります。

右辺の第2項の部分は、先ほど得た不等式から、

\begin{align*} \sum_{n = M +1}^\infty \frac{1}{n^2 – x} \leq \sum_{n = M +1}^\infty \frac{1}{(n- M)^2} \end{align*}

となります。\(k = n -M\) とすることで、

\begin{align*} \sum_{n = M +1}^\infty \frac{1}{(n- M)^2} = \sum_{k = 1}^\infty \frac{1}{k^2} < \infty \end{align*} となります。従って、

\begin{align*} \sum_{n = 1}^\infty \frac{1}{n^2 – x} < \infty \end{align*}

となります。 以上のことをまとめると、\(x\) は「\(1\) 以上の平方数」でないところで収束します。

おまけ

例えば\(x = 37\) のときの\(\frac{1}{n^2 – x}\) の値をグラフで見てみましょう。

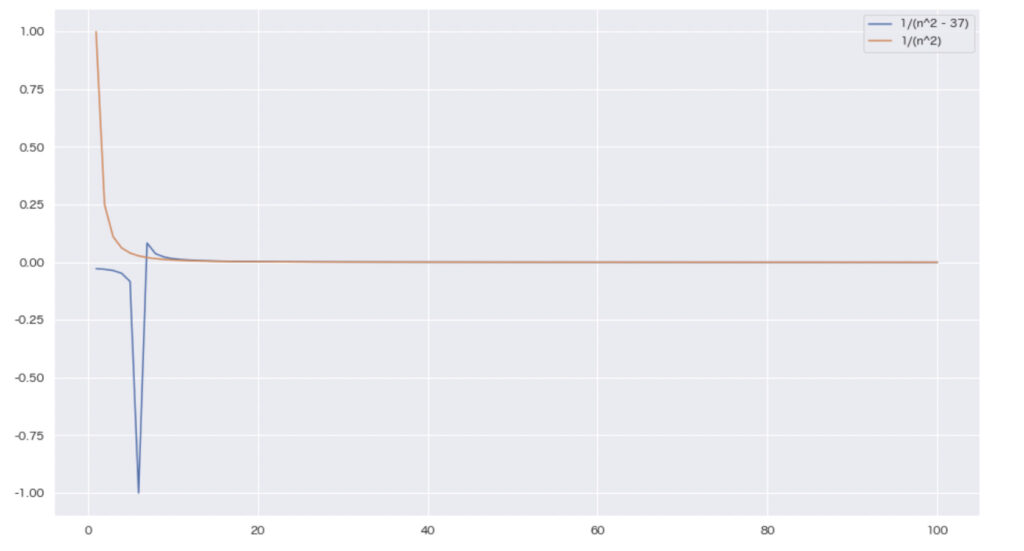
結局のところ、\(n^2\) が十分大きいところでは、\(n^2 – x\) はほとんど\(n^2 \) なんですね。

あわせて読みたい記事