ポートフォリオのリスク分散効果の証明を2資産でわかりやすく解説

投資ポートフォリオにおけるリスク分散効果を、具体的な2資産の例を使ってシンプルに解説します。

ポートフォリオのリスク分散効果の証明を2資産状況わかりやすく解説

投資ポートフォリオとは何かを簡単におさらいしましょう。投資ポートフォリオは、投資家が所有する異なる種類の資産群のことを指します。これらは株式、債券、不動産、現金など、あらゆる種類の資産から成り立っています。

ポートフォリオのリスク分散効果とは、ポートフォリオのリスクが、ポートフォリオを構成する資産のリスクの投資比率に応じた単なる加重平均よりも小さくなることを意味しています。

あくまで、単なる加重平均よりも小さくなることが非自明なのであって、安全資産と危険資産の両方を保持していれば、ポートフォリオのリスクが中程度になるということ自体はほとんど明らかです。

このとき、

が成立します。このことは、ポートフォリオのリスクが、それぞれの資産のリスクの単なる加重平均よりも小さくなることを意味しています。また、2つの金融資産のリターンの相関係数が1未満であるときは、真に不等号が成り立つことも確認できます。

予備知識：相関係数が-1以上1以下であること

命題を証明するためには、相関係数が-1以上1以下であることを思い出しておく必要があります。証明が気になる方は以下の記事をご参照ください。

リスク分散効果の証明

\begin{align*} R_p = w R_A + (1- w) R_B\end{align*}
と定められていることを思い出しておきましょう。

\begin{align*} V(R_p) &= w^2 V(R_A) + (1-w)^2 V(R_B) + 2 w(1-w) \rho \sqrt{V(R_A)}\sqrt{V(R_B)}
\\&=w^2 V(R_A) + (1-w)^2 V(R_B) \\&\quad + 2w(1-w)\sqrt {V(R_A)}\sqrt{V(R_B)} – 2w(1-w)\sqrt{V(R_A)}\sqrt{V(R_B)}
\\&\quad + 2 w(1-w) \rho \sqrt{V(R_A)}\sqrt{V(R_B)}
\\&= \left( w \sqrt{V(R_A)} + (1-w) \sqrt{V(R_B)}\right)^2
\\&\quad + 2w(1-w)(\rho – 1)\sqrt {V(R_A)}\sqrt{V(R_B)}
\\&\leq \left( w \sqrt{V(R_A)} + (1-w) \sqrt{V(R_B)}\right)^2 \end{align*}

という式が得られます。最後の不等号は、\(\rho \leq 1\) より\(\rho – 1 \leq 0\) であることに注意すると、

\begin{align*} 2w(1-w)(\rho – 1)\sqrt {V(R_A)}\sqrt{V(R_B)} \leq 0\end{align*}

であることから従います。従って、\(\frac{1}{2}\)乗すると、

\begin{align*} \sqrt{V(R_p)} \leq w \sqrt{V(R_A)} + (1-w) \sqrt{V(R_B)} \end{align*}

が得られます。

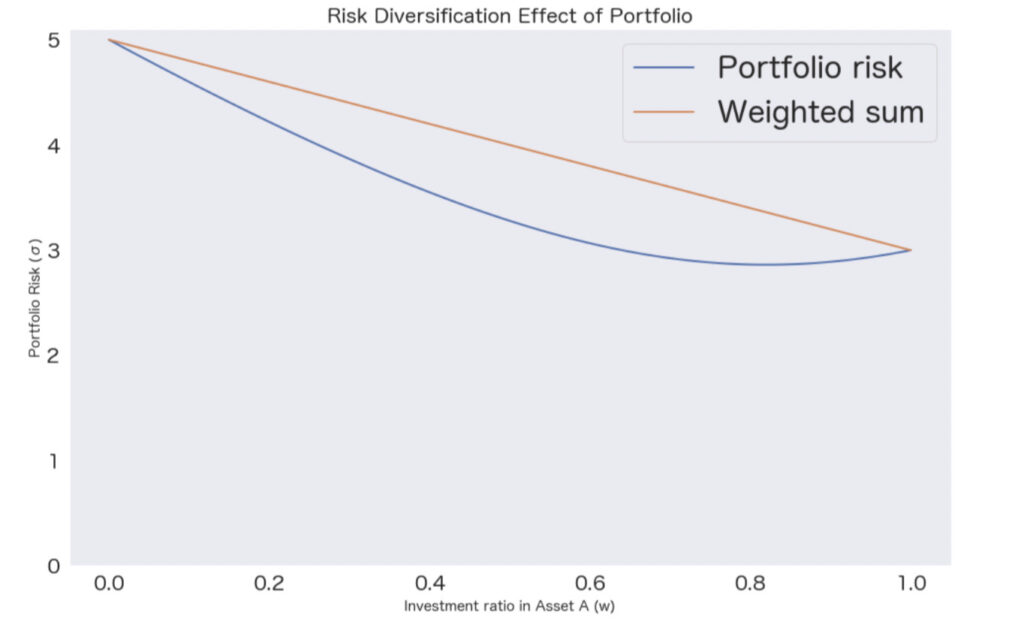
実際、リスク3の資産Aとリスク5の資産Bで、相関係数が0.3であるものに対して、

横軸を資産Aへの投資比率としたとき、ポートフォリオのリスクは青色で記述された下に凸のグラフとなります。

また、オレンジ色のグラフはA, Bのリスクの単なる加重平均を表しています。

視覚的にも、ポートフォリオのリスクが、それぞれの資産のリスクの単なる加重平均よりも小さくなることがみてとれます。

おまけ：相関係数が1の場合は凸結合になる

\(\rho = 1\) の場合（またその場合に限る）、

\begin{align*} V(R_p) = \left( w \sqrt{V(R_A)} + (1-w) \sqrt{V(R_B)}\right)^2\end{align*}

が等号で成り立つので、

\begin{align*} \sqrt{V(R_p)} = w \sqrt{V(R_A)} + (1-w) \sqrt{V(R_B)} \end{align*}

と、ぴったり凸結合と一致します。