投資機会集合と効率的フロンティアを図と数式でわかりやすく解説

2資産による投資機会集合(investment-opportunity-set)と効率的フロンティア(Efficient Frontier、有効フロンティア)を図を用いて解説します。ポートフォリオ理論の中心的な要素であり、投資を行う上での戦略決定において重要な役割を果たします。

2資産の投資機会集合を数式でわかりやすく解説

次のような状況を考えましょう。

以下の等式を得ることができます。

\begin{align*} &\mu = w \mu_A + (1- w) \mu_B \\ & \sigma = \sqrt{w^2 \sigma_A^2 + (1-w)^2 \sigma_B^2 + 2w(1-w) \rho \sigma_A \sigma_B } \end{align*}

さて、\(\mu, \sigma\) は\(w\) に依存して定まる値です。そこで、\(w\)をパラメータとして

\begin{align*} c:[0,1] \rightarrow \mathbb R^2; w \mapsto (\sigma (w), \mu(w)) \end{align*}

という曲線を平面\(\mathbb R^2\)で考えることにします。この曲線、あるいは曲線の像のことを資産A, Bによる投資機会集合といいます。

投資機会集合の性質

投資機会集合はどのような図になるかを考えてみましょう。

\begin{align*} c:[0,1] \rightarrow \mathbb R^2; w \mapsto (\sigma (w), \mu(w)) \end{align*}

の始点と終点を考えます。始点では\(w = 0\) ですので、資産Aへの投資比率は0です。従って、ポートフォリオは資産Bそのものと一致します。また、終点では\(w = 1\) ですので、資産Bへの投資比率は1です。従って、ポートフォリオは資産Aそのものと一致します。

\(w\) を0から1へ変化させることで、\(\mu\) は\(\mu_A\) と\(\mu_B\) の加重平均ですので、両値の間を変化します。一方で、\(\sigma\)は\(\sigma_A\) と\(\sigma_B\) の加重平均よりも小さくなることがリスク分散効果からわかりますので、両値の間よりも小さくなり得ます。リスク分散効果については以下の記事で数式を用いて証明しています。

資産A, Bによる投資機会集合を実際に平面で視覚化すると以下のようになります。

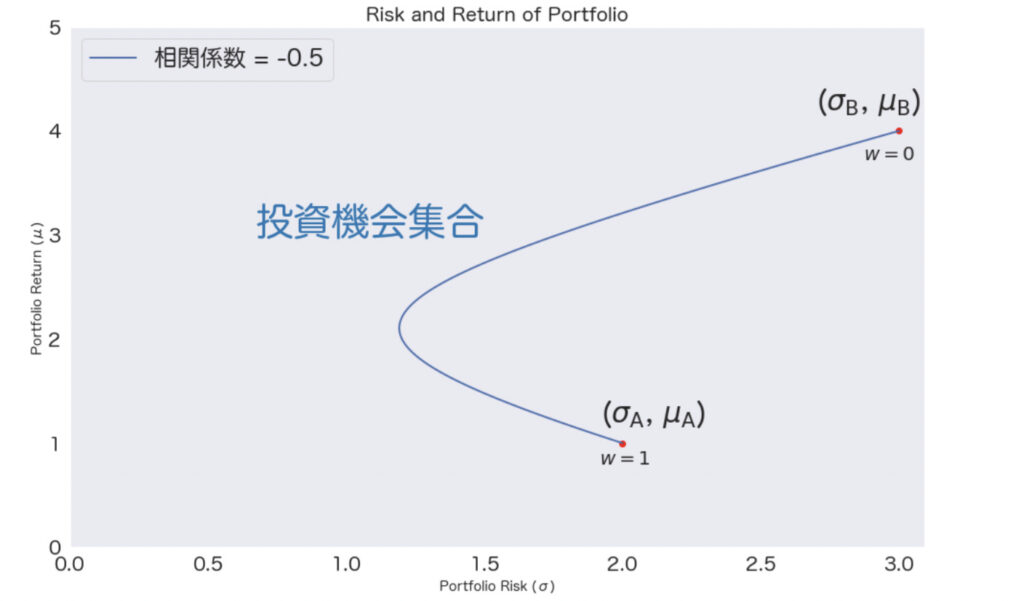
効率的フロンティアとは

効率的フロンティアは

• 同じリターンを得るために最小のリスクをとるポートフォリオ

または

• 同じリスクレベルで最大のリターンを得るポートフォリオ

の集まりのことです。

このことを理解するために、まずは効率的フロンティアでない部分について考えてみましょう。投資機会集合を視覚化すると分かるように、「絶対その投資はしないだろう」という部分が存在することがわかります。それはどこかというと、ポートフォリオとしてリスクは等しいにも関わらずリターンが小さいところです。以下の図でいうところの、赤い点線の部分に該当します。

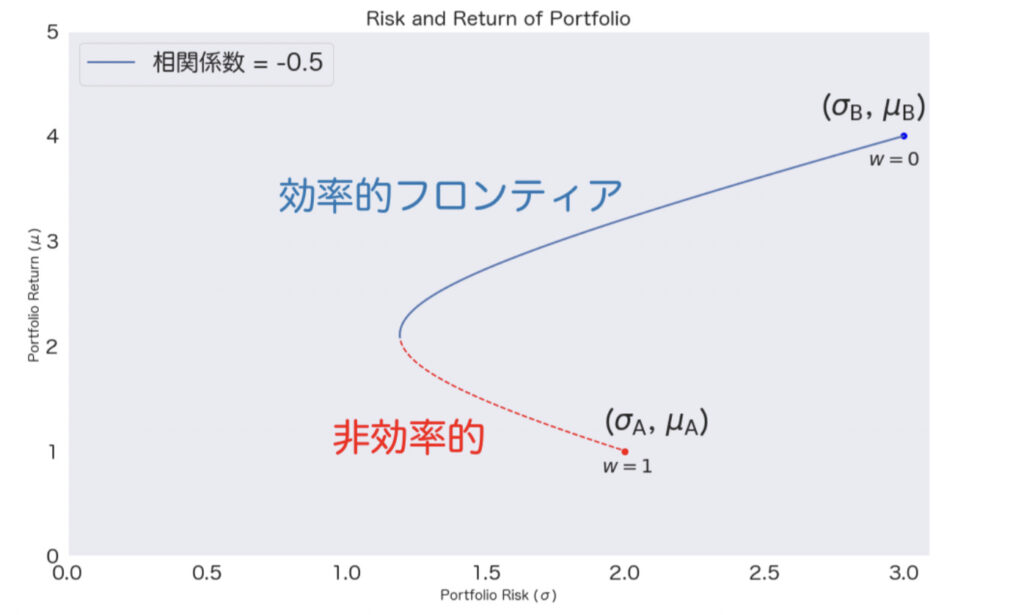
そして、効率的フロンティアとは、投資機会集合のうち、

\begin{align*} \{(\sigma(w), \mu(w)) \in \mathbb R^2 \mid \forall w^\prime, \,\, \sigma(w^\prime) = \sigma(w) \Rightarrow \mu(w^\prime) \leq \mu(w) \}\end{align*}

の部分のことを指します。つまり、同じリスクを取るならば、最も高いリターンを追求したいという投資家の思考を反映したものが、効率的フロンティアです。

投資機会集合の具体例を図で視覚的に解説

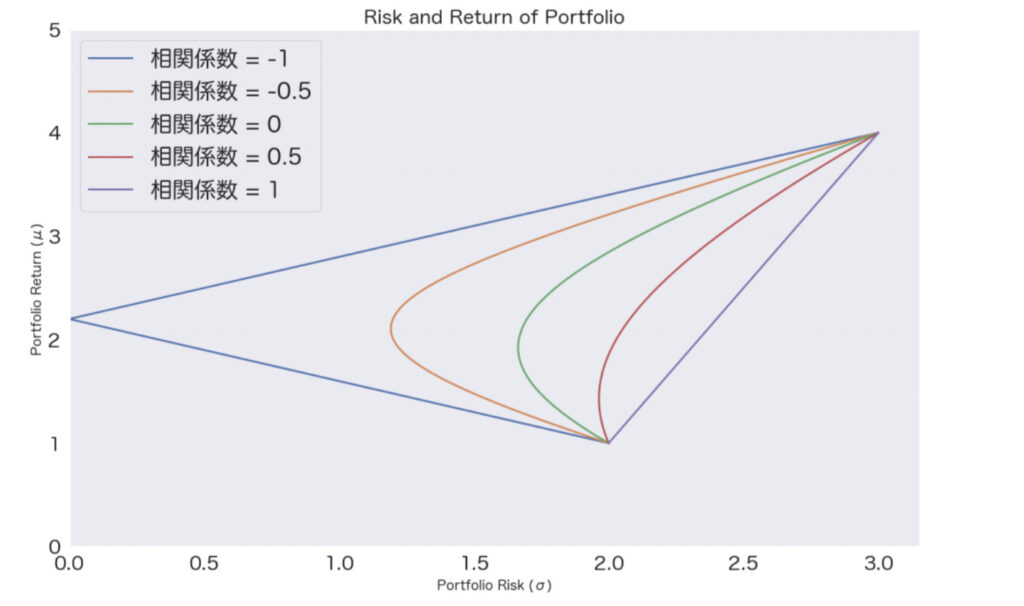
このような具体的な状況で、投資機会集合は上記のように視覚化することができます。

あわせて読みたい記事